信安数学基础一些算法的C语言实现

• 用c实现欧几里得算法,Miller-Rabin 素性检测,求一次同余方程和求素数原根.原理和实现都挺简单,简单记录一下代码吧

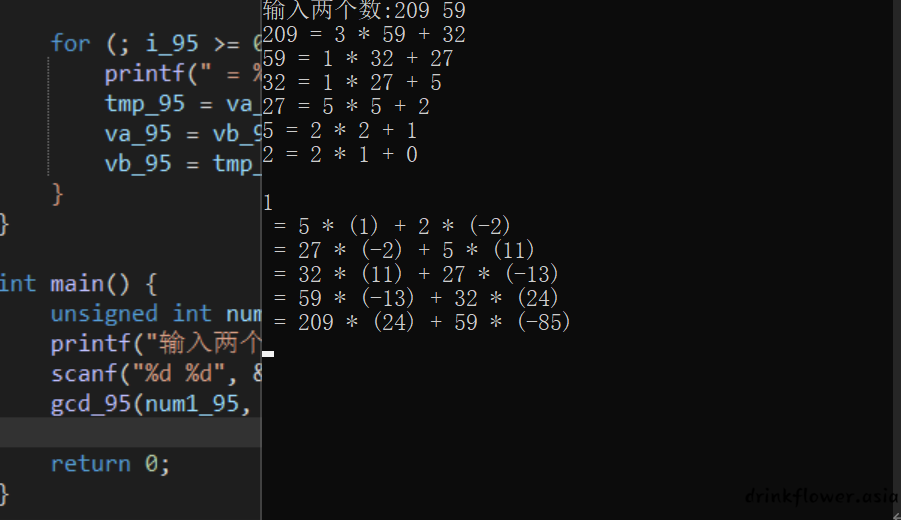
欧几里得算法的实现

#include <stdio.h>

void gcd_95(unsigned int num1_95, unsigned int num2_95) {
    int a_95[32], b_95[32];
    int va_95;
    int vb_95;
    int tmp_95;
    int i_95 = 0, j_95 = 0;

    a_95[0] = num1_95;
    b_95[0] = num2_95;

    while (a_95[i_95] % b_95[i_95] != 0) {
        printf("%d = %d * %d + %d\n", a_95[i_95], a_95[i_95] / b_95[j_95], b_95[j_95], a_95[i_95] % b_95[j_95]);
        i_95++;
        j_95++;
        a_95[i_95] = b_95[j_95 - 1];
        b_95[j_95] = a_95[i_95 - 1] % b_95[j_95 - 1];
    }
    printf("%d = %d * %d + %d\n\n", a_95[i_95], a_95[i_95] / b_95[j_95], b_95[j_95], a_95[i_95] % b_95[j_95]);

    i_95--;
    j_95--;
    va_95 = 1;
    vb_95 = -a_95[i_95] / b_95[j_95];
    printf("%d", a_95[i_95] % b_95[j_95]);

    for (int q=1; i_95 >= 0, j_95 >= 0; i_95--, j_95--) {
        if(q==1)printf("= %d * (%d) + %d * (%d)\n", a_95[i_95], va_95, b_95[j_95], vb_95);
        else printf(" = %d * (%d) + %d * (%d)\n", a_95[i_95], va_95, b_95[j_95], vb_95);
        q++;
        tmp_95 = va_95;
        va_95 = vb_95;
        vb_95 = tmp_95 - a_95[i_95 - 1] / b_95[j_95 - 1] * vb_95;
    }
}

int main() {
    unsigned int num1_95, num2_95;
    printf("输入两个数:");
    scanf("%d %d", &num1_95, &num2_95);
    gcd_95(num1_95, num2_95);

    return 0;
}

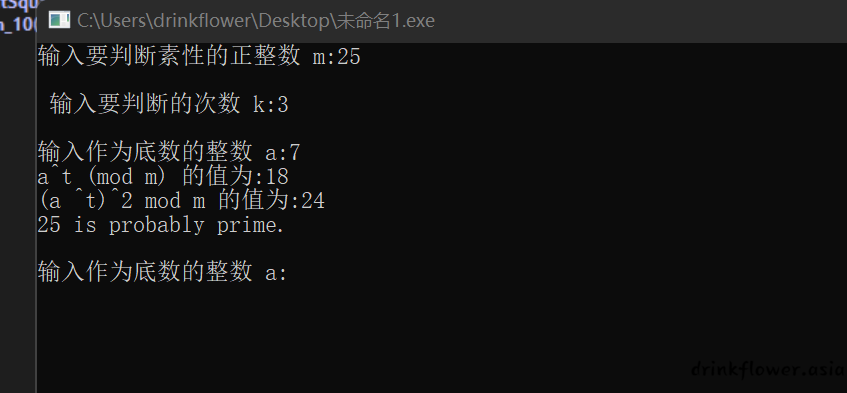
Miller-Rabin 素性检测算法

#include<stdio.h>
long long ModRepeatSquare(int base, int exponent, int modulus) {
    long long result = 1;
    base = base % modulus;

    while (exponent > 0) {
        if (exponent % 2 == 1) {
            result = (result * base) % modulus;
        }
        exponent /= 2;
        base = (base * base) % modulus;
    }

    return result;
}

// Miller-Rabin素性检测的函数（MillerRabin_10）
int MillerRabin_10(int a_10, int m_10) {
    int n = m_10 - 1;
    int s = 0;
    int i;
    long long result;

    // 将 n - 1 表示为 2^s * d 的形式
    while (n % 2 == 0) {
        n /= 2;
        s++;
    }

    printf("a^t (mod m) 的值为:%lld\n", ModRepeatSquare(a_10, n, m_10));
    result = ModRepeatSquare(a_10, n, m_10);

    // 计算 a^t (mod n) 是否等于 ± 1
    if (result == 1 || result == m_10 - 1) {
        return 1;  // 可能是素数
    }

    printf("(a ^t)^2 mod m 的值为:%lld\n", (result * result) % m_10);

    // 计算 (a^t)^(2^i) (mod n) 是否等于 -1
    for (i = 0; i < s - 1; i++) {
        result = (result * result) % m_10;

        if (i != 0) {
            printf("(a ^t)^(2^%d) mod m 的值为:%lld\n", i + 1, result);
        }

        if (result == m_10 - 1) {
            return 1;  // 可能是素数
        }
    }

    return 0;  // 是合数
}

int main() {
    int m, a, k;
    int i;
    int flag = 1;

    // 读入数据
    printf("输入要判断素性的正整数 m:");
    scanf("%d", &m);
    printf("\n 输入要判断的次数 k:");
    scanf("%d", &k);
    printf("\n");

    // 进行多次检测
    for (i = 0; i < k; i++) {
        printf("输入作为底数的整数 a:");
        scanf("%d", &a);

        // 判断结果并输出
        if (MillerRabin_10(a, m)) {
            printf("%d is probably prime.\n\n", m);
        } else {
            printf("%d is composite.\n\n", m);
            flag = 0;
        }

        if (flag == 0) {
            break;
        }
    }

    return 0;
}

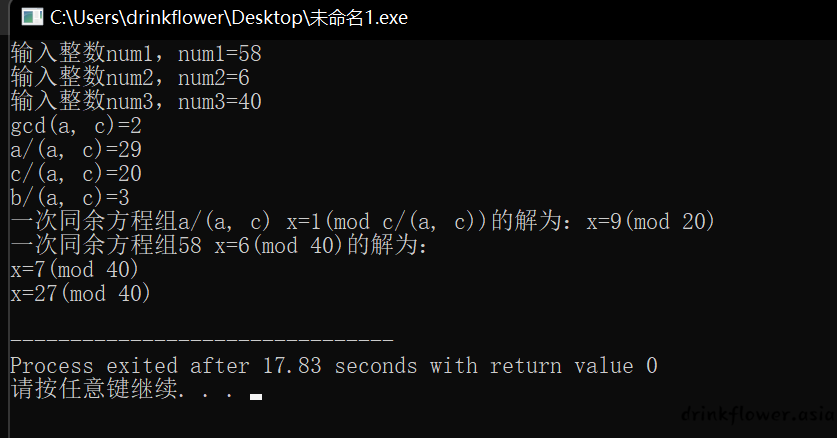
求一次同余方程

#include<stdio.h>

long int eu_95(long int a, long int b, long int* x, long int* y)
{
    if (b == 0)
    {
        *x = 1;
        *y = 0;
        return a;
    }
    long int r = eu_95(b, a % b, x, y);
    long int temp = *x;
    *x = *y;
    *y = temp - a / b * (*y);
    return r;
}

long int dr_95(long int a, long int n)
{
    long int x, y;
    long int r = eu_95(a, n, &x, &y);
    if (r == 1)
        return (x % n + n) % n;
    else
        return -1;
}

int main() {
    long int num1, num2, num3;
    long int x_95 = 0, y_95 = 0;
    printf("输入整数num1，num1=");
    scanf("%ld", &num1);
    printf("输入整数num2，num2=");
    scanf("%ld", &num2);
    printf("输入整数num3，num3=");
    scanf("%ld", &num3);
    long int gcd = eu_95(num1, num3, &x_95, &y_95);
    if (num2 % gcd == 0) {
        long int a1 = num1 / gcd, m1 = num3 / gcd, b1 = num2 / gcd;
        printf("gcd(a, c)=%ld\n", gcd);
        printf("a/(a, c)=%ld\n", num1 / gcd);
        printf("c/(a, c)=%ld\n", num3 / gcd);
        printf("b/(a, c)=%ld\n", num2 / gcd);
        printf("一次同余方程组a/(a, c) x=1(mod c/(a, c))的解为：x=%ld(mod %ld)\n", dr_95(a1, m1), m1);
        long int x1_95 = dr_95(a1, m1);
        printf("一次同余方程组%ld x=%ld(mod %ld)的解为：\n", num1, num2, num3);
        long int n = (num2 / gcd * x1_95) % m1;
        while (n < num3)
        {
            printf("x=%ld(mod %ld)\n", n, num3);
            n += m1;
        }
    }
    else {
        printf("无解\n");
    }
    return 0;
}

求素数原根

#include <stdio.h>
int pri_95(int n) {
    for (int i = 2; i <= n / 2; i++) {
        if (n % i == 0) {
            return -1;
        }
    }
    return 1;
}
int cal_95(int m, int a) {
    for (int i = 2; i <= m; i++) {
        if (m % i == 0 && a % i == 0) {
            return -1;
        }
    }
    return 1;
}
int find_95(int m,int a) {
    int r = 1;
    int jie = 0;
    int array[1000];
    int y = 0;
    for (int i = 1; i <= m - 1; i++) {
        r = r * a;
        r = r % m;
        if ((m-1) % i == 0) {
            array[y] = i;
            y++;
            if (r == 1&&jie==0) {
                jie = i;
            }
        }
    }
    int count = 0;
    printf("ord=%d\n",jie);
    for (int i = 2; i <m ; i++) {
        int tp = 1;
        for (int j = 1; j <= m-1; j++) {
            tp = tp *i;
            tp = tp % m;
            if (tp == 1 && j != m - 1) {
                goto end;
            }
        }
        if (tp == 1) {
            count = count + 1;
            printf("找到mod %d的一个原根g=%d\n", m, i);
        }
    end:
        printf("");
    }
    printf("mod %d的原根总共有%d个", m,count);
    return 0;
}
int main() {

    int n;
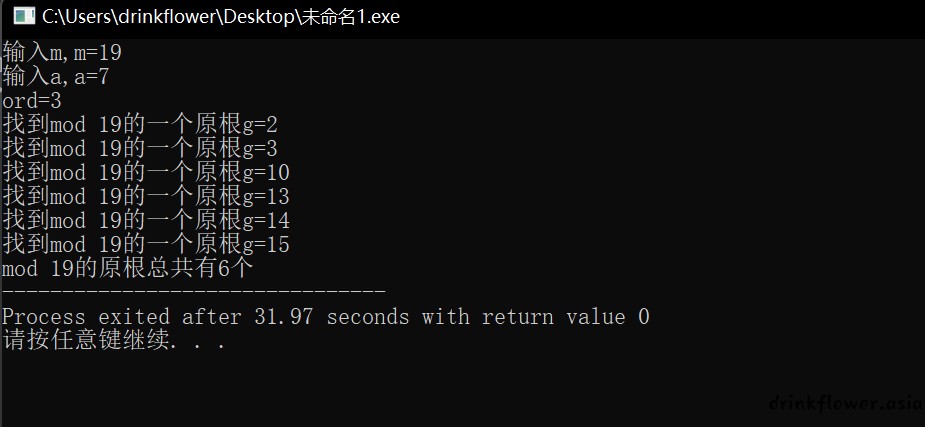
    printf("输入m,m=");
    scanf("%d", &n);
    while (pri_95(n) < 0) {
        printf("这不是素数!请重新输入m,m=");
        scanf("%d", &n);
    } 
    printf("输入a,a=");
    int a;
    scanf("%d", &a);
    while (cal_95( a, n)<0) {
        printf("不互素,请重新输入a,a=");
        scanf("%d", &a);
    }
    find_95(n, a);
    return 0;
}